The first derivative of a function is a fundamental concept in calculus that measures how that function changes as its input varies. It provides crucial information about the rate of change of a quantity at any given point, indicating whether the function is increasing or decreasing and the steepness of that change.
At its core, the first derivative signifies the rate of change of a function’s output in response to small changes in its input. For example, when considering a function that describes the position of an object over time, its first derivative represents velocity, demonstrating how quickly the position alters.
Geometrically, the first derivative corresponds to the slope of the tangent line to the graph of the function at a specific point. A positive slope indicates an increasing function, while a negative slope signifies a decreasing one. When the slope is zero, the function is flat at that point, which might indicate a local maximum or minimum.
The first derivative is denoted using different notations; for instance, if a function is represented as f(x), its first derivative can be expressed as f'(x) or df/dx. A simple example is f(x) = x^2 , where the first derivative is f'(x) = 2x.
This concept has numerous applications across various fields. In physics, for example, it is used to derive velocity from a position function, while in economics, it can represent marginal cost or revenue.
When examining ventricular pressure waveforms, which describe the changes in pressure within the heart’s ventricles during the cardiac cycle, the first derivative becomes especially significant. The waveform illustrates how ventricular pressure rises and falls during different phases of the cardiac cycle, such as contraction (systole) and relaxation (diastole). Analyzing this waveform is essential for understanding cardiac function and hemodynamics.
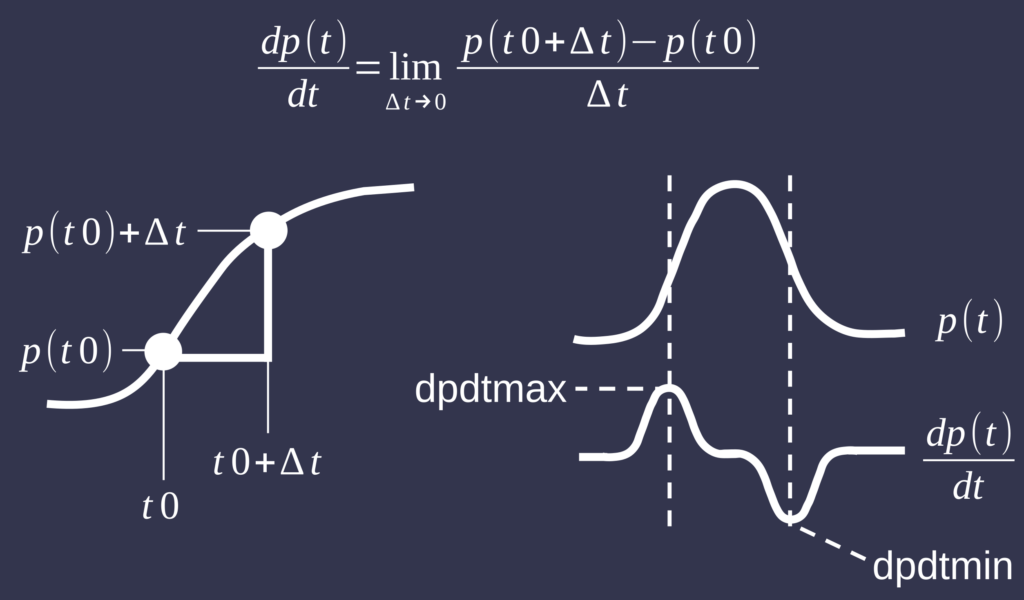
In this context, the first derivative, denoted as dp/dt, represents the rate at which ventricular pressure changes over time. It provides insight into how quickly the pressure is rising or falling at any moment.
A particularly important aspect is the maximum dp/dt (dpdtmax), which refers to the peak rate of increase in ventricular pressure during systole. To identify this maximum rate, one typically calculates the first derivative of the pressure waveform data to observe where the derivative reaches its highest value. This peak signifies the point of fastest pressure increase and reflects the heart’s contractility.
dpdtmax is load dependent due to the effects of preload and afterload on cardiac contractility. Increased preload enhances ventricular stretch, allowing for more forceful contractions and a higher dpdtmax, elevated afterload increases the resistance the heart must overcome which can also cause an increase in dpdtmax. A better variable for contractility is the load independent end-systolic elastance Ees.
In hemodynamics, the standard unit for dp/dt is millimeters of mercury per second (mmHg/s).
